Inverse sine function

Definition

The inverse of the sine function is called the inverse sine function.

The sine function represents a value of the ratio of the length of opposite side to length of hypotenuse at the respective angle of a triangle, whereas the inverse sine function represents an angle for a value of the ratio of the length of opposite side to length of the hypotenuse of the same triangle.

Function

The inverse sine is written in short form as $\large \arcsin$ or $\large \sin^{-1}$ in mathematics.

According to the definition of the inverse sine function, the inverse sine function is expressed in mathematical form as follows.

$\large \sin^{-1} \normalsize \Bigg[\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}\Bigg]$ $\,=\,$ $Angle \, of \, the \, Triangle$

It can also be written in the following form.

$\large \arcsin \normalsize \Bigg[\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}\Bigg]$ $\,=\,$ $Angle \, of \, the \, Triangle$

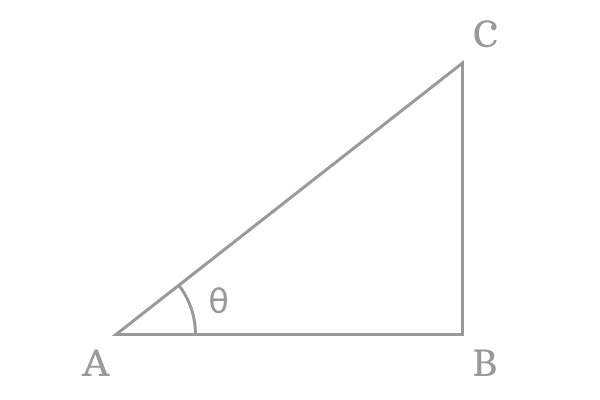
For example, $\Delta BAC$ is a right angled triangle and its angle is $\theta$. $\overline{BC}$ and $\overline{AC}$ are opposite side and hypotenuse, and their lengths are $BC$ and $AC$ respectively.

The arc sine is expressed in mathematical form as follows for the $\Delta BAC$.

$\large \sin^{-1} \normalsize \Big(\dfrac{BC}{AC}\Big) \,=\, \theta \,\,\,$ or $\,\,\, \large \arcsin \normalsize \Big(\dfrac{BC}{AC}\Big) \,=\, \theta$

Assume, the quotient of the length of the opposite side by the length of hypotenuse is $x$.

Then, $\large \sin^{-1} x \,=\, \theta \,\,\,$ or $\,\,\, \large \arcsin x \,=\, \theta$

The $\sin^{-1} x$ or $\arcsin x$ is the representation of the inverse sine function in mathematical form.

Example

The functionality of the arcsine or inverse sine function can be understood geometrically from this example.

1. Draw a horizontal line by using a ruler and $D$ is the left side endpoint of the line.
2. Take Protector, and draw a line of $30^\circ$ angle from point $D$.
3. Use compass and set the distance between needle point to pencil point to $12$ centimetre with the help of a ruler and then draw an arc on $30$ degrees angle line from point $D$. The intersecting point of arc and $30^\circ$ line is called point $E$.
4. Use set square, and draw a perpendicular line to horizontal line from point $E$. The line perpendicularly intersected the horizontal line at point $F$.

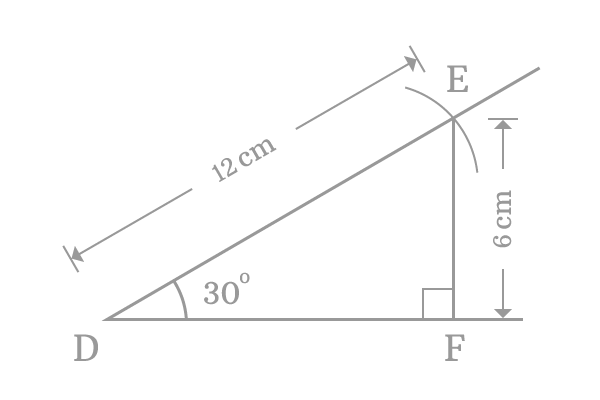
The geometric procedure is constructed a right angled triangle $DEF$ and its angle is $30^\circ$. Now, measure, the length of the opposite side $\overline{EF}$ by using a ruler. You will observe that it is $6 \, cm$ exactly.

The functionality of the inverse sine function is expressed in mathematically in the following way.

$\sin^{-1} \Big(\dfrac{6}{12}\Big) \,=\, 30^\circ$

$\implies$ $\require{cancel} \sin^{-1} \Big(\dfrac{\cancel{6}}{\cancel{12}}\Big) \,=\, 30^\circ$

$\therefore \,\,\,\,\,\,$ $\sin^{-1} (0.5) \,=\, 30^\circ$

It can also be expressed in another form.

$\therefore \,\,\,\,\,\,$ $\arcsin (0.5) \,=\, 30^\circ$

The inverse of the sine function is given that the angle of the right angled triangle is $30^\circ$ for the value $0.5$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.