A point where an angle is made by the intersection of two lines, is called vertex of an angle.
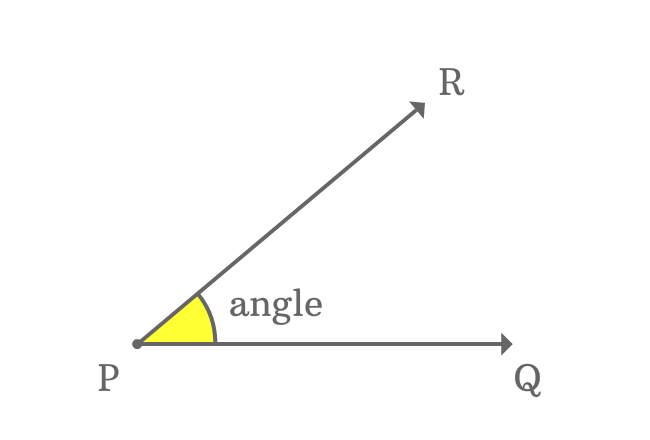
$\overrightarrow{PQ}$ and $\overrightarrow{PR}$ are two lines and they both meet each other at their common point $P$.
The intersection of the rays $\overrightarrow{PQ}$ and $\overrightarrow{PR}$ formed an angle at point $P$. The point is the only reason for forming the angle between them. Therefore, the point $P$ is called vertex of the angle.
So, every point where an angle is made by the intersection of the lines, is known as vertex of the angle.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved