A set of values for which the function is defined, is called the domain of a function.
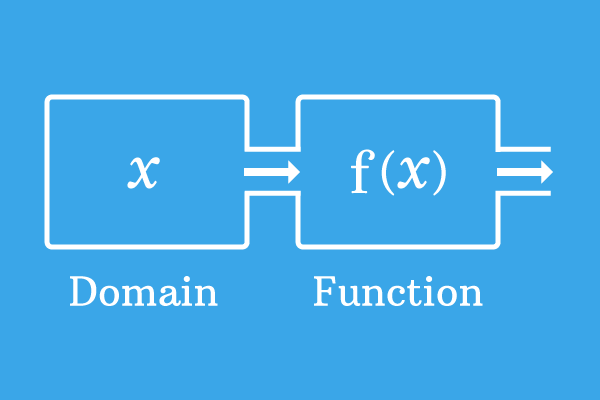
The domain of a function is a set basically.
In mathematics, every function gives corresponding values for different values of variable but in some cases, the functions are undefined for one or some values of variable because the functions cannot give us associated values.
The collection of values of variable for which the given function is defined is called the domain of a function. It is represented graphically and mathematically as a set in mathematics.
Let’s take $f(x)$ is a function and $x$ is a variable. Assume, the function $f(x)$ is defined for the elements $a, b, c, d$ and $e$. The associated values of the function are given here.
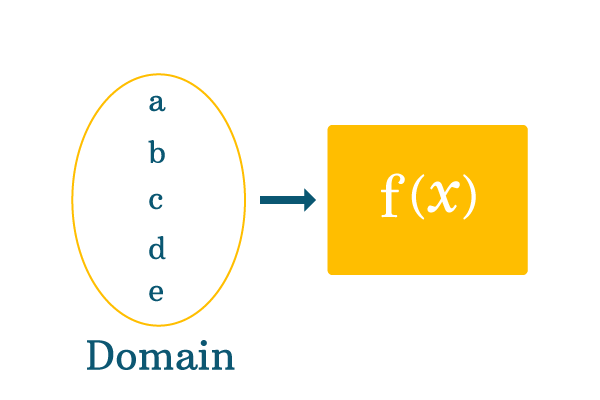
The values of function are $f(a)$, $f(b)$, $f(c)$, $f(d)$ and $f(e)$ for $x$ is equal to $a$, $b$, $c$, $d$ and $e$ respectively. The collection of the elements $a$, $b$, $c$, $d$ and $e$ is called the domain of the function.
$x = \{a, b, c, d, e\}$
$f(x) = \dfrac{1}{x+2}$
Substitute all the real numbers to determine the domain of this function.
For example, Take $x = 0$ and evaluate the function.
$x = 0$ $\implies$ $f(0) = \dfrac{1}{0+2} = \dfrac{1}{2}$
For $x$ is equal to zero, the value of the function is $\dfrac{1}{2}$. Now, substitute positive real numbers and obtain their associated values.
$x = 1$ $\implies$ $f(1) = \dfrac{1}{1+2} = \dfrac{1}{3}$
$x = 2$ $\implies$ $f(2) = \dfrac{1}{2+2} = \dfrac{1}{4}$
$x = 3$ $\implies$ $f(3) = \dfrac{1}{3+2} = \dfrac{1}{5}$
$x = 4$ $\implies$ $f(4) = \dfrac{1}{4+2} = \dfrac{1}{6}$
$x = 5$ $\implies$ $f(5) = \dfrac{1}{5+2} = \dfrac{1}{7}$
$\vdots$
Thus, the function is defined for all the positive real numbers.
Now, substitute all the negative real numbers one by one and test the functionality of this function.
$x = -1$ $\implies$ $f(-1) = \dfrac{1}{-1+2} = \dfrac{1}{1} = 1$
$x = -2$ $\implies$ $f(-2) = \dfrac{1}{-2+2} = \dfrac{1}{0} = \infty$
For the value $x$ is equal to $-2$, the example function becomes undefined. Hence, the value of $x$ should not be equal to $-2$. Continue testing the function by substituting the remaining negative real numbers.
$x = -3$ $\implies$ $f(-3) = \dfrac{1}{-3+2} = \dfrac{1}{-1} = -1 $
$x = -4$ $\implies$ $f(-4) = \dfrac{1}{-4+2} = \dfrac{1}{-2} = -\dfrac{1}{2}$
$x = -5$ $\implies$ $f(-5) = \dfrac{1}{-5+2} = \dfrac{1}{-3} = -\dfrac{1}{3}$
$\vdots$
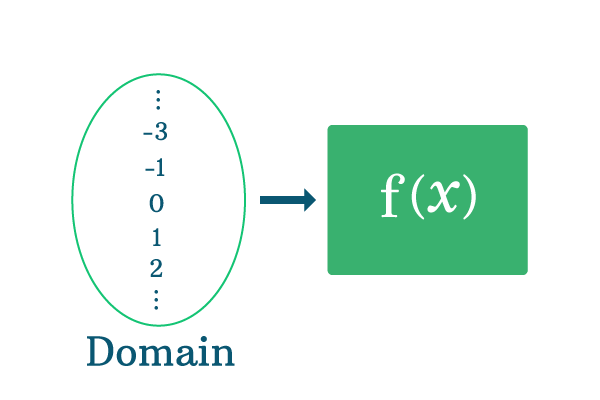
Now, collect all the elements as a set but ignore $x$ is equal to $-2$. Therefore, the collection of elements is called the domain of this function.
$x = \{\cdots -4, -3, -1, 0, 1, 2, 3, \cdots\}$
According to the set theory, the real numbers group is simplify denoted by $R$ but it contains $-2$. Hence, it should be subtracted from it. Therefore, the domain of the function is simplify written as $R-\{-2\}$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved