Proof of ${(a+b+c)}^2$ formula in Geometric Method

Proof

The a plus b plus c whole square formula is derived in algebraic form by geometrical approach as per the areas of square and rectangle.

Evaluating Area of a Square

1. Take a square and divide the square vertically into three different parts by drawing two lines. The lengths are $a$, $b$ and $c$ respectively.
2. Divide the square horizontally into three parts but the lengths of them should also be $a$, $b$ and $c$ respectively.
3. The length of each side is $a+b+c$. Therefore, the area of the square is $(a+b+c) \times (a+b+c)$ $\,=\,$ ${(a+b+c)}^2$

Calculating Areas of Internal Squares and Rectangles

The square whose area is $a$ plus $b$ plus $c$ whole square, is divided as three squares and six rectangles.

1. Length of each side of three squares are $a$, $b$ and $c$. So, the areas of them are $a^2$, $b^2$ and $c^2$ respectively.
2. The lengths of sides of two rectangles are $a$ and $b$. So, the area of each rectangle is $ab$.
3. The lengths of sides of two rectangles are $c$ and $a$. So, the area of each rectangle is $ca$.
4. The lengths of sides of two rectangles are $b$ and $c$. So, the area of each rectangle is $bc$.

Obtaining the a+b+c whole square formula

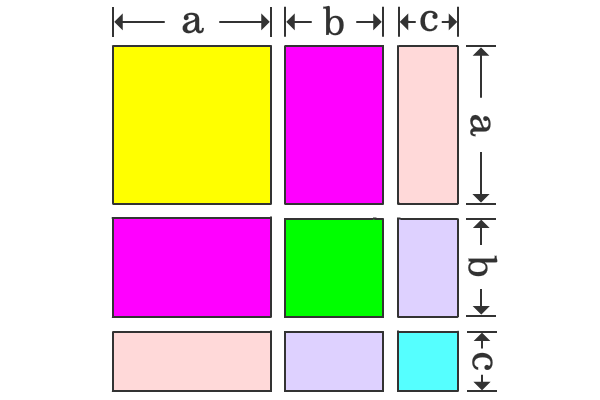
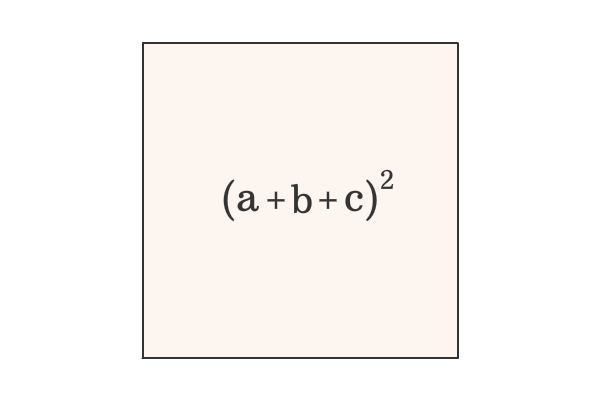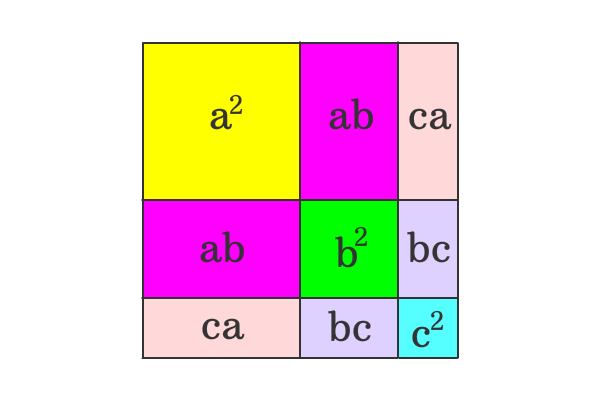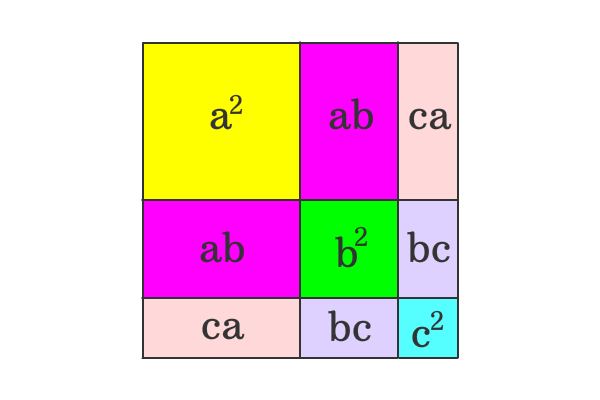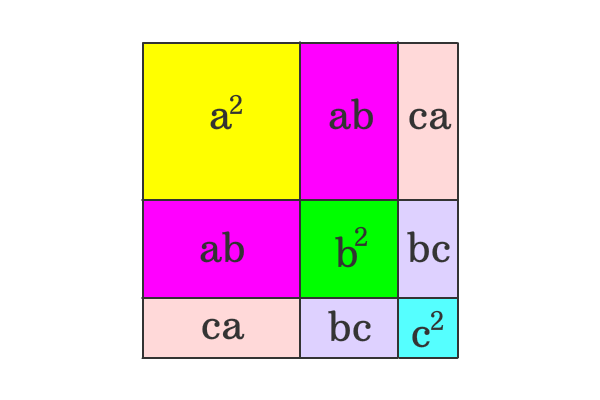
The area of whole square is ${(a+b+c)}^2$ geometrically.

The whole square is split as three squares and six rectangles. So, the area of whole square is equal to the sum of the areas of three squares and six rectangles.

${(a+b+c)}^2$ $\,=\,$ $a^2+ab+ca$ $+$ $ab+b^2+bc$ $+$ $ca+bc+c^2$

Now, simplify the expansion of the $a+b+c$ whole square formula to obtain its expansion in simplified form.

Thus, the expansion of a plus b plus c whole square is proved in algebraic form by the geometrical approach in mathematics.

$\,\,\, \therefore \,\,\,\,\,\, {(a+b+c)}^2$ $\,=\,$ $a^2+b^2+c^2$ $+$ $2ab+2bc+2ca$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.